Have you ever come across a phrase like "xxxxxx is equal to x 2" and felt a little puzzled? You are not alone, you know. It can seem like a secret language, especially if you are not used to seeing numbers and letters put together in that particular way. This kind of expression, while a bit unusual in its writing, actually opens up a really interesting conversation about how we talk about math. It points us to some basic ideas that are pretty central to how numbers work and how we figure things out with them, you see.
This phrasing, "xxxxxx is equal to x 2," is a way some folks might write or think about a more common math problem. It is about an unknown value, which we call 'x', and how that value relates to the number two. What it really means is that you are looking for a number that, when multiplied by itself a certain way, gives you two. This idea of finding an unknown is what math problems are often about, more or less.
So, we are going to break down what this expression stands for, how you might solve it, and why understanding these sorts of mathematical puzzles can be quite useful in everyday thinking. It is really just about making sense of symbols and what they tell us to do with numbers. We will try to make it all very clear, so you can get a good handle on it, as a matter of fact.
Table of Contents
- What Does "xxxxxx is equal to x 2" Really Mean?
- Why This Equation Matters
- How to Solve for 'x' When xxxxxx is equal to x 2
- Common Questions About This Kind of Math Problem
- Putting It All Together
What Does "xxxxxx is equal to x 2" Really Mean?
When you see "xxxxxx is equal to x 2," it might look like a typo or a strange code at first glance. However, based on some common ways people talk about math problems, and from what we have seen in certain discussions, this expression points to a very specific type of equation. It is essentially a way of writing "x times x times x is equal to 2." That is the core idea, you know.
Decoding the Notation
The phrase "xxxxxx" is a stand-in for 'x' multiplied by itself multiple times. In this particular case, it means 'x' is multiplied by itself three times. Think of it like this: if you write 'x' three times and put multiplication signs between them, you get x * x * x. This is what "xxxxxx" is trying to convey in a more casual, perhaps shorthand, way. So, "xxxxxx is equal to x 2" really means x * x * x = 2. This is often written in a much shorter way as x³ = 2, where the small '3' tells you how many times 'x' is multiplied by itself. It is a neat little trick, that.
This way of writing things, with the 'x' repeated, is not the standard way math books show it. But it does help us think about what is happening. It makes it very clear that 'x' is involved in a multiplication problem with itself. It is a bit like saying "go-go-go" instead of "go quickly," you see. Both mean to move fast, but one shows repetition for emphasis. Here, the repetition shows how many times 'x' is used in the multiplication, which is rather important.
The Idea of Powers
When you multiply a number by itself several times, we call that using a "power." So, x * x * x is 'x' to the power of three, or 'x cubed'. The 'cubed' part comes from geometry, actually. Imagine a box where each side has a length of 'x'. The space inside that box, its volume, would be x * x * x. So, "xxxxxx is equal to x 2" is asking us to find the side length of a cube that has a volume of 2. It is a pretty neat connection, that.
This idea of powers is very common in math and in the everyday world. For example, when we talk about square feet for an area, we are using a power of two (length times width, where length and width are often the same for a square). Here, with 'cubed,' we are dealing with three dimensions. So, you know, it is not just some abstract math idea; it has real-world shapes tied to it. This connection can make the idea feel a bit more concrete, sometimes.
Why This Equation Matters
Understanding an equation like "xxxxxx is equal to x 2" goes beyond just solving a math problem. It helps us think about how numbers behave and how we can figure out things we do not know. This kind of problem is a good example of what algebra is all about. It is a way to find missing pieces of information using what we already have, more or less.
Finding the Unknown
Every time you solve for 'x' in an equation, you are playing a sort of detective game. You are given some clues, and you need to use those clues to figure out the mystery number. In this case, the clue is that 'x' multiplied by itself three times gives you 2. The job is to find what 'x' must be. This skill of figuring out unknowns is very useful, not just in school, but in many parts of life. For instance, if you are trying to figure out how much something costs per person, you are solving for an unknown, in a way. It is a fundamental process, really.
This process also helps us understand inverse operations. If multiplication is happening on one side of the equation, we need to do the opposite, or inverse, operation to get 'x' by itself. For 'cubing' a number, the opposite is taking the 'cube root'. It is like undoing something. If you add, you subtract to undo. If you multiply, you divide to undo. If you cube, you take the cube root. It is a system, you see, and knowing the system helps a lot, you know.
More Than Just Numbers
Equations like x³ = 2 help us see that not all answers are simple, whole numbers. The number 'x' that solves this equation is not something you can write down as a simple fraction or a whole number. It is what we call an irrational number, which means its decimal goes on forever without repeating. This shows us that the world of numbers is much bigger and more varied than just the numbers we count with. It is quite fascinating, in fact.
This understanding can help us appreciate the richness of mathematics. It shows that math can describe things that are not always neat and tidy. For example, the diagonal of a square or the circumference of a circle often involve these kinds of numbers. So, this one little equation, "xxxxxx is equal to x 2," opens up a whole field of thought about different kinds of numbers and how they show up in the world around us. It is pretty cool, that.
How to Solve for 'x' When xxxxxx is equal to x 2
So, we know "xxxxxx is equal to x 2" means x³ = 2. Now, how do we actually find the value of 'x'? The way to do this is by using a special mathematical operation called the cube root. This is the opposite of cubing a number, as we talked about earlier. It is about finding the number that, when multiplied by itself three times, gives you the number inside the root symbol. It is a straightforward process, you know.
The Cube Root Operation
To solve x³ = 2, you need to take the cube root of both sides of the equation. The cube root of x³ is simply 'x'. The cube root of 2 is written as ³√2. So, the solution is x = ³√2. This is the exact answer. It is a specific number, even if it looks a bit different from numbers you might be used to seeing. It is kind of like saying "the square root of 2" instead of "1.414..." because the exact form is often more precise, you see.
Finding the cube root of a number means you are looking for a base number. This base number, when used as a factor three times in a multiplication, results in the number under the root sign. For instance, the cube root of 8 is 2, because 2 * 2 * 2 equals 8. The cube root of 2 is a bit more involved, as it is not a whole number. It is a number that, when multiplied by itself three times, gets you exactly 2. This is the definition, basically.
Using a Calculator
Since ³√2 is an irrational number, you will usually need a calculator to get a decimal approximation. Most scientific calculators have a cube root button, or a general root button where you can specify the root (like 'x-root-y' or 'y-root-x'). If you type in 2 and then press the cube root button, you will get a number that starts with 1.2599 and goes on and on. This is the approximate value of 'x'. It is very useful for practical applications where you need a number you can actually use, for example, in measurements. You know, you can't really measure with an infinite decimal, so approximations help a lot.
When you use a calculator, you are getting a close estimate. For most purposes, this estimate is perfectly fine. For example, if you are building something and need to know the side length of a cube with a volume of 2 cubic units, you would use this decimal value. It helps us bridge the gap between exact mathematical answers and real-world needs. So, it is a practical tool, really, that helps us apply the math we are learning.
Common Questions About This Kind of Math Problem
Here are some questions people often ask about expressions like "xxxxxx is equal to x 2," which really means x³ = 2.
What does "xxxxxx is equal to x 2" mean in math?
This phrase is a way to say "x multiplied by itself three times is equal to 2." In standard math writing, it is x³ = 2. The repeated 'x's are just a simple way to show that 'x' is being used as a factor three times in a multiplication. It is about finding a number that, when cubed, gives you 2. That is the core idea, you know.
How do you solve an equation like "x cubed equals 2"?
To solve x³ = 2, you need to find the cube root of 2. This is the inverse operation of cubing a number. So, you would write the solution as x = ³√2. If you need a decimal value, you can use a calculator, which will give you approximately 1.2599. It is a straightforward process once you know the right operation to use, you see.
Why is understanding cubic equations important?
Understanding cubic equations, like x³ = 2, is important for several reasons. They appear in many areas of science and engineering, like calculating volumes, understanding physics problems, or even in computer graphics. They also help us learn about different types of numbers, including irrational numbers, which are numbers that cannot be written as simple fractions. So, they help us understand the wider world of numbers and how they describe things around us, basically. You can learn more about equations and their solutions on our site, which is pretty neat.
Putting It All Together
The expression "xxxxxx is equal to x 2," while it might look a bit different, simply asks us to solve for 'x' in the equation x³ = 2. This involves finding the cube root of 2, which is a number that, when multiplied by itself three times, gives us 2. It is a fundamental idea in algebra, and it shows us how we can find unknown values in math problems. It also opens our eyes to the idea of different kinds of numbers, like those that go on forever in their decimal form. So, it is a pretty neat concept, that.
Understanding these basic mathematical ideas helps us make sense of the world around us. From figuring out volumes to working with more complex scientific problems, the ability to solve for unknowns is a skill that helps in many areas. So, the next time you see something like "xxxxxx is equal to x 2," you will know exactly what it means and how to approach it. It is all about breaking down the problem into smaller, understandable parts, which is a good skill to have, you know. To learn more about how different powers work, you could check out a resource like Math Is Fun's page on exponents. You can also explore more about mathematical notation and its history here on our pages.
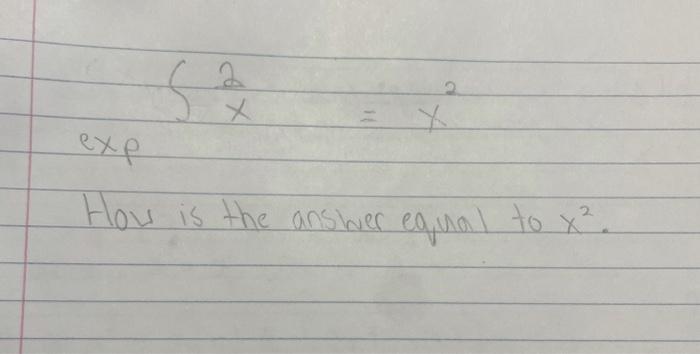
(x-6).jpg)

Detail Author:
- Name : Prof. Ambrose Bartoletti Sr.
- Username : ransom57
- Email : herzog.claud@kuvalis.com
- Birthdate : 2004-12-25
- Address : 59466 Dach Centers Apt. 865 East Elias, AL 44960-7442
- Phone : 920.745.4941
- Company : Schmeler PLC
- Job : Transportation Attendant
- Bio : Non quam deleniti et dolor porro. Provident officiis necessitatibus sed perspiciatis in animi. Iure et fuga exercitationem aspernatur.
Socials
facebook:
- url : https://facebook.com/nienowj
- username : nienowj
- bio : Facilis suscipit voluptas dolore vel laborum a qui cupiditate.
- followers : 3498
- following : 2636
twitter:
- url : https://twitter.com/jacinto.nienow
- username : jacinto.nienow
- bio : Et ad voluptatem quidem debitis possimus et. Consequatur aspernatur enim mollitia sequi. Eum eos sint voluptatem quae sunt beatae officiis mollitia.
- followers : 4959
- following : 2659